√100以上 底 面積 公式 170691-円錐 底面積公式

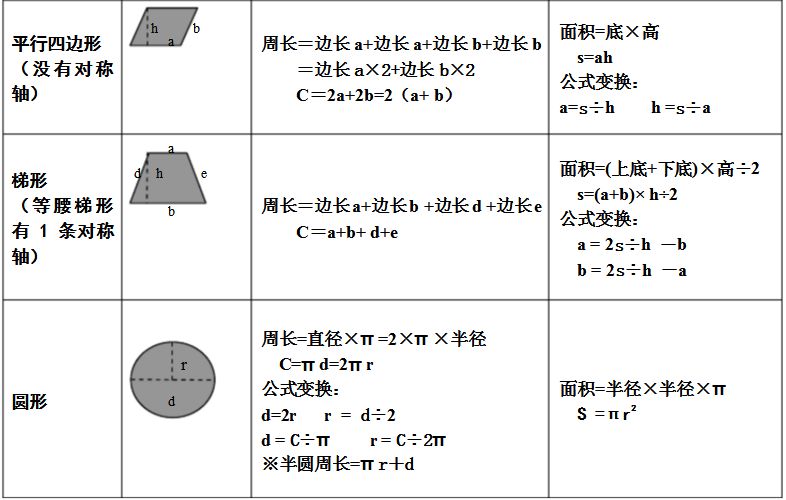
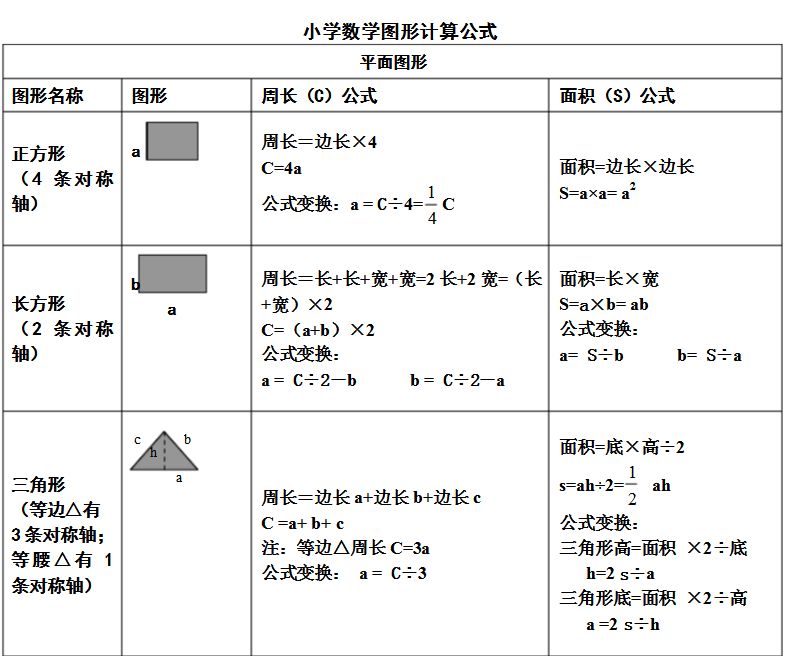
計算公式 面積 長方形面積=長×寬 = 正方形面積=邊長 2 = 平行四邊形面積=底×高; 三角形、平行四邊形、梯形，多邊形面積公式怎麼記？ （上底＋下底）× 高 ÷ 2 ，這可能是小學最複雜的面積公式。 多邊形的面積也可以用拼貼法的方式來聯想嗎？ 正方形、長方形、三角形、平行四邊形、梯形，那麼多面積公式怎麼記得住啊？ ① 帶孩子 正方形 面積=a的平方 周長=4a 平行四邊形 面積=ah 周長=2 (ab) 三角形 面積=05ah 周長=abc 梯形 面積=05 (ab)h 周長沒有公式 6 梅之絕影 長方形 面積=長*寬=ab 周長= (長寬)*2=2 (ab) 正方形 面積=邊長*邊長=a的平方 周長=邊長*4=4a 平行四邊形 面積=底*=高ah 周長= (底

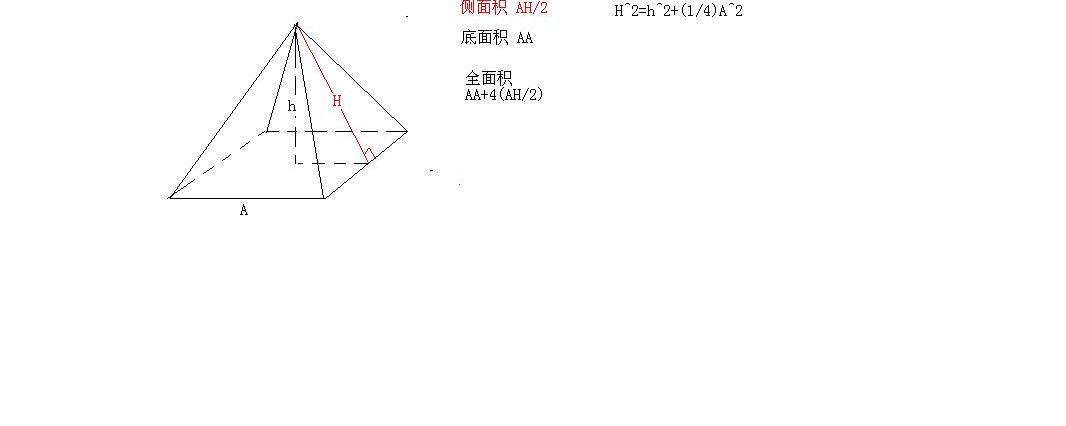
正四棱锥底面积公式 扒拉扒拉

円錐 底面積公式

円錐 底面積公式- 橢圓面積公式 ： S=πab 橢圓面積定理：橢圓的面積等於圓周率（π）乘該橢圓長半軸長（a）與短半軸長（b）的乘積。 橢圓面積公式 應用實例 橢圓的長半軸為8cm，短半軸為6cm，假設π=314，求該橢圓的面積。 答：S=πab=314*8*6=（cm²） ひし形（菱形）の面積の求め方の公式って？？ こんにちは！この記事をかいているKenだよ。ドタキャンはきついぜ。 ひし形（菱形）の面積の求め方の公式 は、 大きく分けて、 2つ あるんだ。 対角線×対角線÷2 ってやつ。 それと、 底辺×高さ って公式だ。

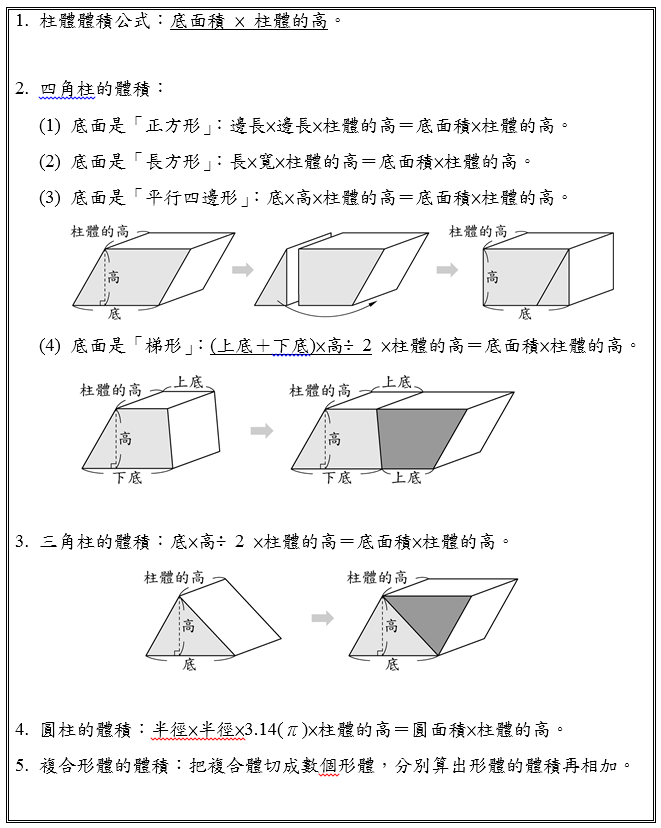
體積公式參考 Geogebra

 なぜ、どんな形をした三角形でも、その面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求まるのでしょうか。 形がちがう2種類の「底辺 5 c m 高さ 2 c m の三角形」を通じてみていきましょう。 ※1マス 1 c m 初めに、同じ形 体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方（公式） を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め面积公式圆环面积 圆环面积外圆面积内圆面积 (圆周率X大半径的平方圆周率X小半径的平方\圆周率X (大半径的平方小半径的平方) 已知圆环的外直径为D，圆环厚度（即外内半径之差）为d。 d=Rr，Dd=2R (Rr)=Rr，可由第一、二种方法推得 S=π (Rr)× (Rr)=π (Dd

长方体或正方体底面的面积叫做 底面积 长方体 和正方体的底面积求法 长方体的底面积=长x宽 正方体的底面积=棱长x棱长 所以，长方体和 正方体 的体积也可以这样来计算： 长方体（或正方体）的体积=底面积x高 如果用字母s表示底面积，上面的公式可以写成 公式 四角柱の体積＝底面積（底面の四角形の面積）×高さ を求めることができるでしょう。 体積を求める上でのポイント 注意が必要なのは、この底面積たる四角形の面積を求める際に、しっかりとそれを導くことができるか、つまり、四角形に面積を求める公式 ・長方形の面積＝縦 横 ・平行四辺形の面積＝底辺 高さ ・三角形の面積＝底辺 高さ÷2 ・台形の面積＝(上底＋下底) 高さ÷2 ・円の面積＝半径 半径 円周率 体積を求める公式 ・柱体の体積＝底面積×高さ 高さ 底面 下底 上底

3 図形の公式 31 円 円周 l = 2πr r S 面積 S = πr2 32 おうぎ形 弧の長さ l = 2πr × θ 360 r θ S 面積 S = πr2 × θ 360 = 1 2 lr 33 角柱・円柱 表面積= 側面積 底面積×2 側面積= 底面の周× 高さ 体積 V = Sh (S 底面積 h 高さ) S h S h 2 https//skipdreamcom 3 回答 台形の面積の公式は、（上底下底）×高さ÷2ですが、 台形の上底と下底の厳密なきまり、定義のようなものはあるのでしょうか。 一般的な台形は、上底＜下底だと思うのですが、ひっくり返った台形ですと、上底＞下底になりますね。 また 18年9月26日 / 19年1月3日 三角形の面積は「 底辺 高さ 底 辺 × 高 さ ÷ 2 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていき

圆锥底面积公式怎么算 百度经验

长方体底面积公式是什么 全民百科

 底面積05m 2 で0g（→2N）の荷物が床に置かれているとき、床にかかる圧力は0÷05＝400(Pa)となります。 また、1hPa＝100Paです。（400Paなら4hPaになります。） 問題で面積の単位がcm 2 になっているときは、1m 2 ＝cm 2 よりでわってm 2 に換算するか、cm 2 のまま割り算してをかける 4 回答 中学三年生です。 底面積の意味が不明です。 体積を求める公式の中に底面積と書いてあるんですけどこの底面積はどう求めるんですか？ 頭のいいかたよろしくお願いします！ 至急です！ 中学数学 ・ 4,932 閲覧 正三角形の面積の求め方を3ステップで伝授しよう。 さっきの正三角形ABCの面積を求めていくよ。 Step1 頂角から二等分線をおろす 頂角の二等分線を底辺にひいてみよう。 頂角が半分になる線をすーーーっと底辺にひけばいいのさ。 AからBCにむかって二

圓柱體積公式 公式 釋義 圓周率 中文百科全書

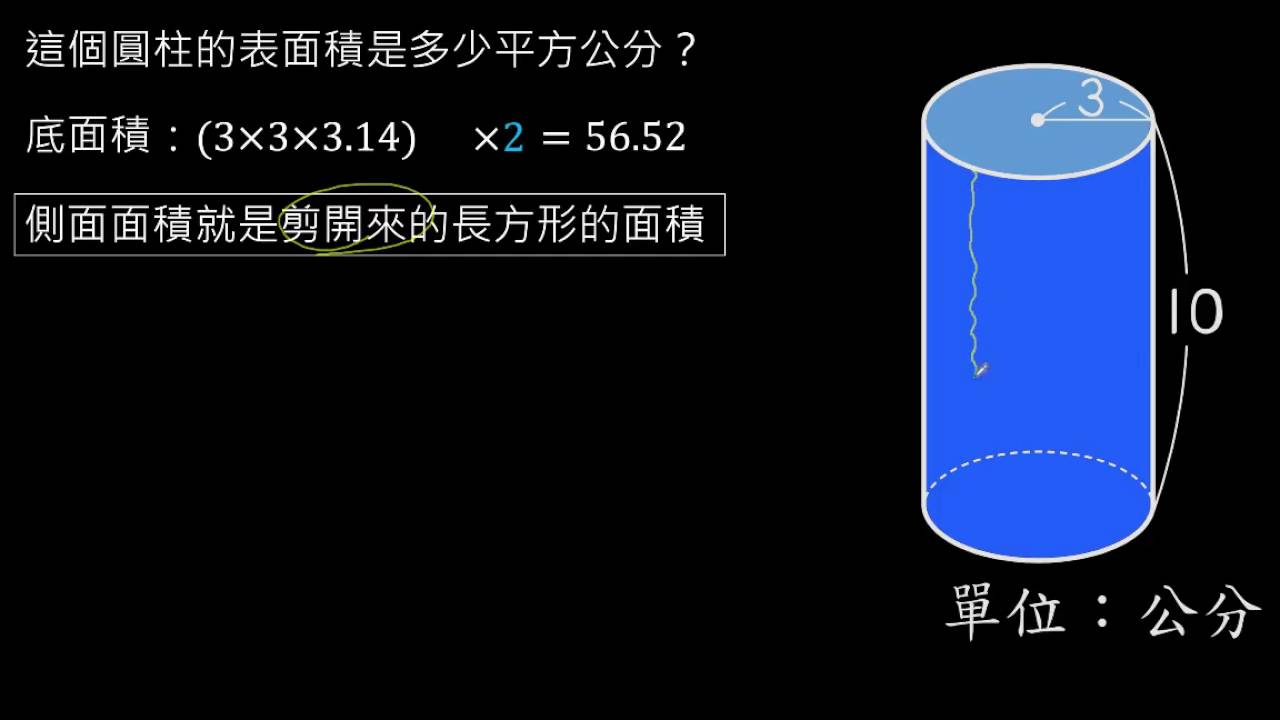
圆柱的表面积公式 趣智分享

圆柱的底面积是一个圆形 那么圆柱的底面积公式就是圆形的计算公式 已知底面直径求底面积：（直径÷2）²×314 已知底面半径求底面积：半径²×314 a²=a×a 扩展资料： 圆柱的两个圆面叫底面，周围的面叫侧面，一个圆柱体是由两个底面和一个侧面组成的。2角柱と円柱 角柱・円柱の体積＝底面積×高さ 角柱・円柱の表面積＝底面積×2側面積 3角すいと円すい台形の公式を使って底面積を求めればいいだけです。 簡単だね！ 〇 四角柱の体積は、底面積を求めて高さをかけるだけ！ 〇 底面積は四角形の種類によって、面積の公式を使い分けてね！

体积公式 快懂百科

底面積乘高等於什麼底面積乘高是什麼體積的計算公式 經驗 摩登站

公式の導き方や、面積計算の問題の解き方は、リンク先のページでご覧になれます。 お使いのブラウザでは JavaScript が無効になっています。 当サイトは数式表示に JavaScript を利用しているため、これを無効にしているとページが正しく表示されません。 底面積は上に記載の通りで求めることができます。 なお側面積は、底面の辺の長さ×高さという公式で求めることができます。 そのため、三角柱の表面積＝底辺×底面の三角形の高さ ＋ 底辺×高さ×3という公式で求めることができるのです。 所以，長方體和正方體的體積也可以這樣來計算：長方體（或正方體）的體積=底面積x高 如果用字母s表示底面積，上面的公式可以寫成： v=sh 底面積 圓柱底面積

正方体的底面积公式是什么 爱问知识人

圓錐體的底面積公式是啥 教育 酷知吧

 続いて、三角柱の表面積の公式は「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた$8cm^2$ですね。 側面積の求め方ですが 「高さ × 底面の周の長さ」で求めることがで では次は公式化してみましょう。 今考えていた四角錐の底面は1辺がaの正方形なので、底面積は、 a×a＝a 2 ですね。 次に高さは、立方体の半分の高さとなっているので、 a×1/2 です。 したがって、底面積と高さを使って公式をつくるためには、平行四邊形的面積 平行四邊形的面積 認識平行四邊形的底和高 三角形的面積 三角形的底、高和面積 梯形的面積 梯形的面積 多邊形的面積 題 1

图文版 小学数学图形的周长 面积 体积公式 圆柱

圆锥的表面积公式 圆锥体的表面积的计算公式是什么 环球信息网

次の計算公式は底が等しい場合に限り成り立つ． 1 log a M log a N= log a MN 2 log a M− log a N= log a MNn 3 n log a M= log a (M n )= log a M n 異なる底で表された対数について，上記のような計算を行うには，あらかじめ底が等しい対数に書き換えておかなければならV = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は 小學數學1~6年級基礎公式及知識整理 三角形的面積＝底×高÷2。 公式 S= a×h÷2 內角和：三角形的內角和＝180度。 圓柱的表（側）面積：圓柱的表（側）面積等於底面的周長乘高。 公式：S=ch=πdh＝2πrh 圓柱的表面積：圓柱的表面積等於底面的周長乘高再加上

填表 底面半径 Cm高 Cm圆柱圆锥体积 Cm3侧面积 Cm2表面积 Cm2体积 Cm3215 6 题目和参考答案 青夏教育精英家教网

非常有用的常用求面積 體積公式 非常有用收藏吧 每日頭條

底面积公式：长方体的底面积=长×宽，正方体的底面积=棱长×棱长，长方体（或正方体）的体积=底面积×高，如果用字母s表示底面积，上面的公式可以写成：v=sh。 常用单位： 立方米、立方分米、立方厘米、立方毫米。 棱长是1毫米的正方体，体积是1立方毫米。両辺にcを底とする対数をとると ここで次の公式を使う そうすると (1)を使って を元に戻すと 証明終 ≪2図による解説≫ のグラフとx軸および， の直線， で囲まれる図形の面積を で表すことにする． つまり， の右側にある面積を で表す． この面積（英語： Area ）是用作表示一個曲面或平面 圖形所佔範圍的量，可看成是長度（一維度量）及體積（三維度量）的二維類比。 對三維立體圖形而言，圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。

底面积公式底面积的含义 扒拉扒拉

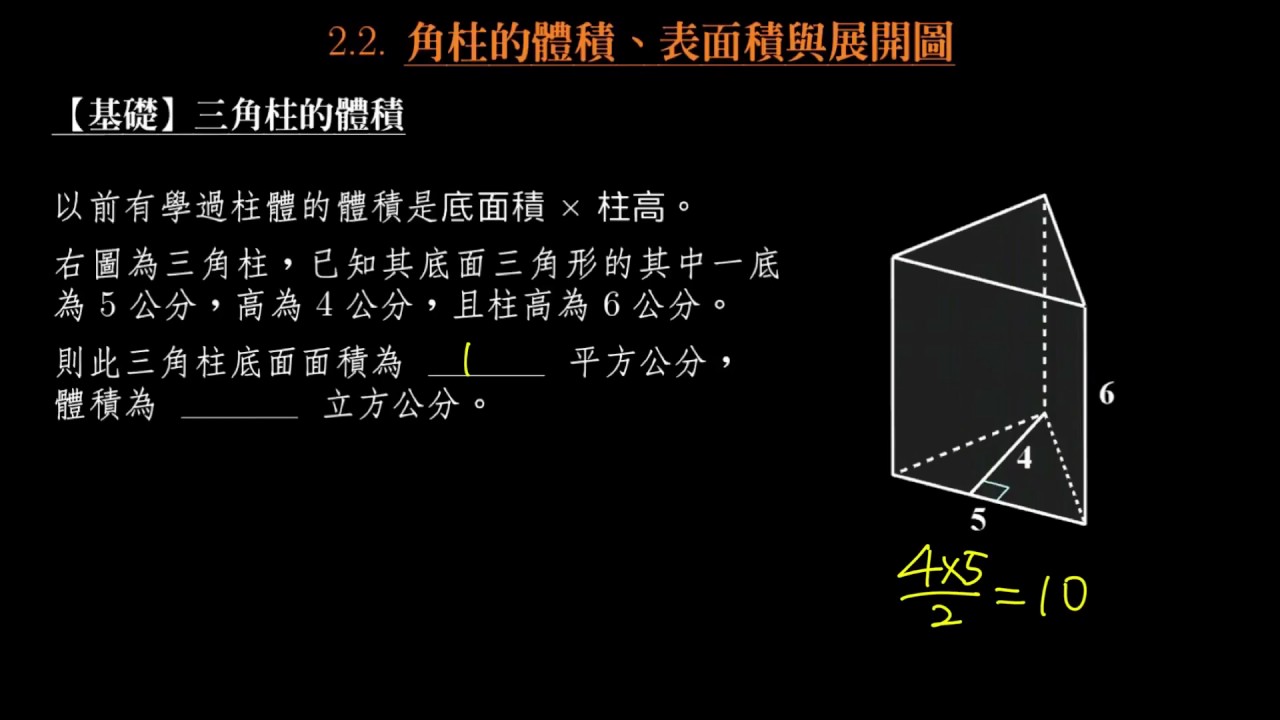
基礎 三角柱的體積 Youtube

 圓柱的總體積=底面積×高。 公式：V=Sh 8圓錐 圓錐的總體積＝底面積×高×1/3 公式：V=1/3Sh 三角形內角和＝180度。 平行線：同一平面內不相交的兩條直線叫做平行線 垂直：兩條直線相交成直角，像這樣的兩條直線，

计算长方形的周长和面积公式 三年级数学上册长方形正方形计算公式及练习 附图形计算公式表 偷得一寸光的博客 Csdn博客

小学四年级的孩子注意了 这份数学公式大全收好 争取考100分 面积

体积公式大全 计算圆的体积公式是什么 环球信息网

圆柱底面积的计算公式 搜狗图片搜索

梯形下底面积公式 搜狗图片搜索

圆柱的一个底面积公式是什么 圆柱的底面积公式是多少是什么 教育新闻网

面積 27 求三角形的 底 的基本練習 Youtube

圆柱的底面积公式 9篇

柱體的體積與表面積 05 另一種長方形體積的計算方式 底面積x 高 Youtube

全网总结最全 17种求三角形面积的公式 从平面到立体 收藏 雪花新闻

C8b2ebb547f0baec3ac1b Jpg

计算长方形的周长和面积公式 三年级数学上册长方形正方形计算公式及练习 附图形计算公式表 偷得一寸光的博客 Csdn博客

圆柱的侧面积公式 趣智分享

圆柱体积公式 百度百科

體積公式參考 Geogebra

圆锥的底面积公式是什么圆锥的底面积公式是什么 朵拉利品网

圆柱的体积怎么计算 圆柱的体积公式是什么 金测评 数码科技家居产品试用体验金分享 评测网站

底面積 底面積是數學用語 一般用于求幾何體的底部面積 華人百科

面积公式 趣智分享

面積 29 求梯形的 底 的基本練習 Youtube

底面积公式 底面积公式文字 伤感说说吧

正四棱锥底面积公式 扒拉扒拉

14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫

长方体底面积公式 扒拉扒拉

长方体底面积公式是什么 爱问教育培训

平方怎么算及面积平方怎么计算 平方怎么算公式是什么

底面积乘高是什么公式底面积乘高是啥公式 天奇生活

圆锥的底面积公式是什么 全民百科

圆柱体表面积 圆柱的表面积公式是什么 圆柱的表面积公式是 明日之子

圆柱底面积怎么求 圆柱底面积怎么算公式 新生活信息网

面积公式 百度百科

1

图文版 小学数学图形的周长 面积 体积公式 圆柱

三角形的面積公式你只知道底乘高除2 其實海倫公式也是相當牛的 壹學 壹學

圆柱底面积公式 搜狗图片搜索

07 圓柱的表面積 Youtube

小学数学公式 面积 体积换算公式 字 小学知识点 小学数学知识点

关于底面积的体积公式 哔哩哔哩 Bilibili

圆柱底面积公式是什么怎么写 30高考网

圆柱底面积公式是什么 求圆柱的底面积公式是什么 我要软文网

呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港

计算面积的公式 妮可辣岛芭 的博客 Csdn博客

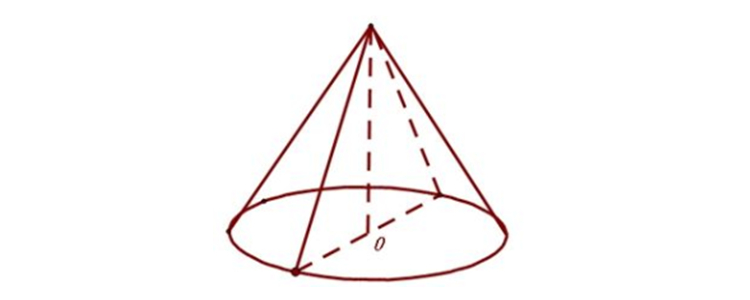
圆锥底面积公式 扒拉扒拉

圆柱体积公式 头条搜索

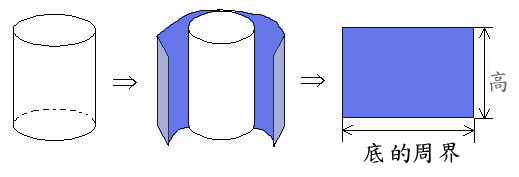
11 面積及體積 Area And Volume 齊齊溫

已知沙堆的体积和高 可直接套用公式 求出沙堆的底面积 网易视频

小学四年级数学图形的周长 面积 体积公式 图文版 熟练运用

圆锥的底面积怎么求计算方法是什么 高三网

关于底面积的体积公式 哔哩哔哩 Bilibili

底面积 快懂百科

底面积 百度百科

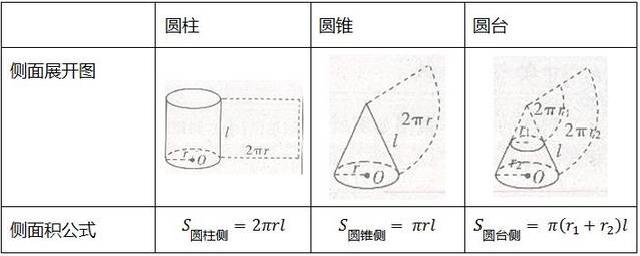
圆柱体的底面积公式是什么 扒拉扒拉

2

正方体的底面积公式 正方体的表面积公式 伤感说说吧

编辑公式字体 初中数学公式 圆柱体面积公式 尚书坊

初中数学 几何 面积与体积公式 维基教科书 自由的教学读本

常用体积面积周长公式 搜狗图片搜索

长方体的体积公式 图文版小学数学图形的周长

表面积公式 体积表面积公式 伤感说说吧

正方形的底面積公式是啥 教育 酷知吧

圆柱底面积公式怎么算 圆柱底面积公式 教育新闻网

圆柱底面积公式 高三网

梯形面积公式求高 梯形面积的计算 已知高面积求上下底之和 尚书坊

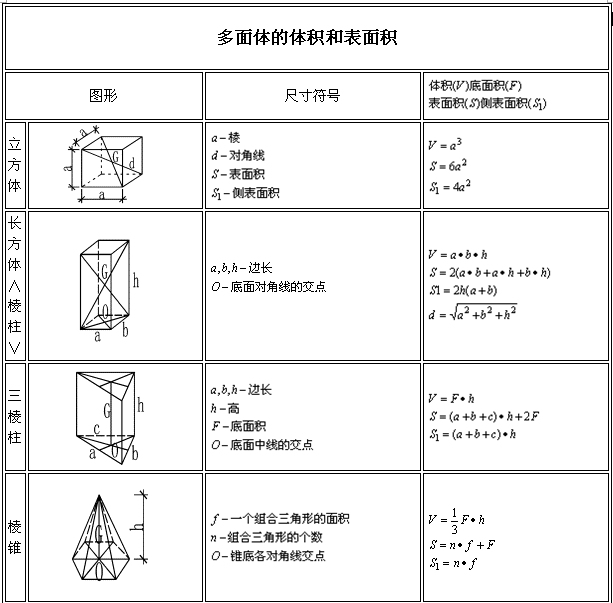
建议收藏 常用图形面积体积计算公式 建筑一生

图形底面积计算公式 第1页 要无忧健康图库

关于底面积的体积公式 哔哩哔哩 Bilibili

圆柱的表面积公式是什么圆柱体积公式 养娃家

圆柱的底面积公式 趣智分享

圆柱的面积公式表面积公式体积公式 相见148

底面积 头条搜索

圆柱底面积公式 圆柱的侧 表 底面积 底面周长 圆的面积 周长公式是什么 物联网独家报道 物联网 物联网时代 中国物联网第一门户 物联中国

1

什么叫圆柱体面积公式是什么 初三网

面積公式表

Image016 Jpg

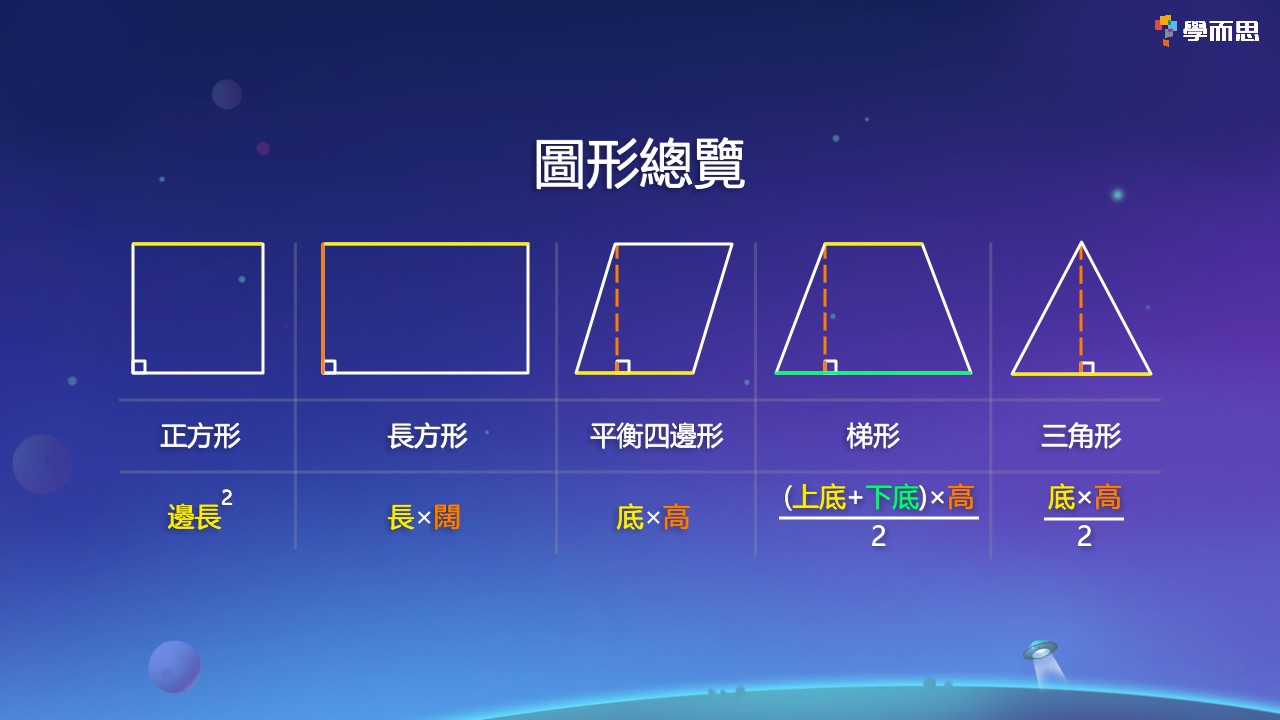
呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港

圆柱的底面积公式 这些一定要熟记

Amc10 数学中的面积公式推证

高中数学 体积表面积公式 哔哩哔哩 Bilibili

台体体积公式 快懂百科

1

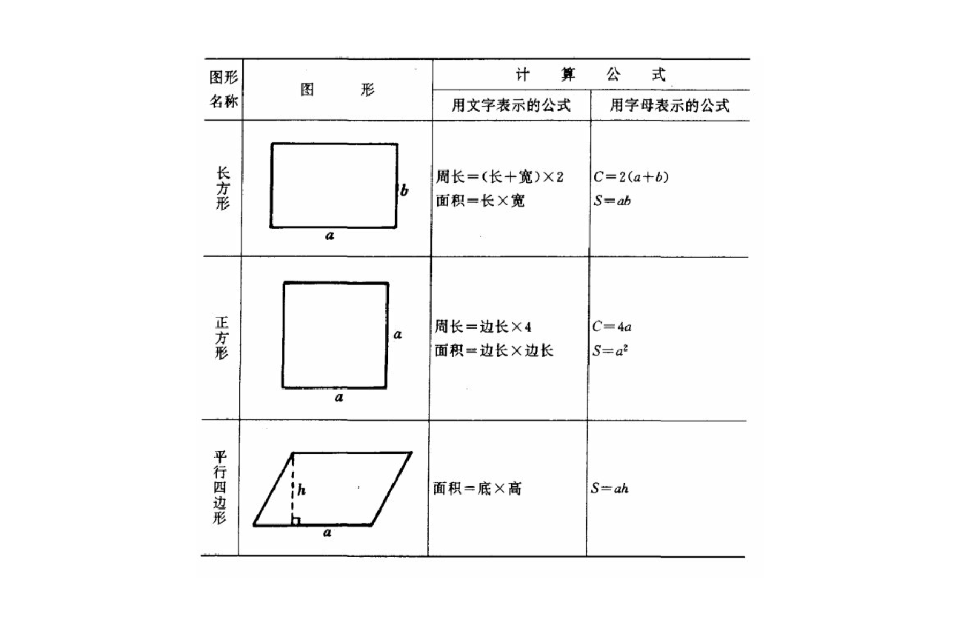
面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書

体积公式面积公式 雨露学习互助

底面積 底面積是現代詞 是一個專有名詞 指的是長方體或正方體底面的面積 百科知識中文網

长方形的面积公式是什么 全民百科

體積公式大全體積公式有哪些 經驗 摩登站

圆柱体积公式和表面积 梯形圆柱体积计算公式 扬帆号

Incoming Term: 底面積公式, 円錐 底面積公式,